I recently just had the concept of heap sort motivated to me in such a fantastic manner that I had to share it.
Before we get into the explanation, sorry it's been a while, I'll try to be more regular with my blog posts!
Let's start off our exploration with the end result. We want to be able to input an array into some function, and for the function to mutate it in a way where the array becomes sorted (that is to say, that a[n] > a[n+1]).
If you had to sit down and solve this problem, one of the easiest ways you could think of it selection sort. I'll write some basic pseudocode so you can get a feeling for how it works.
for i = 0 and i < n
max = -infinity
max_index = -1
for j = 0 and j < n
if a[j] > max
max = a[j]
max_index = j
swap(i, max_index)In more human english, this could be translated as:
For each value in the array
1. Find the maximum value after the current index
2. Swap the value in the current index with the maximum valueThis is incredible simple, but also slow. We have to iterate over every value of the array for every value of the array, so in other words, this runs in O(n^2) time. This seems like a dead end. In order to optimize this, we would need to either:
Number 1 is impossible. No sorting method, even some of the more advanced ones, are able to avoid this step. Number 2 seems impossible, and it actually is impossible if the only assertion we can make about the array is that it is not sorted. If only there was a certain data structure that made it so that accessing the maximum value was really fast...
Oh hey priority queue, how have you been?
A lot of you may never have met my good friend Priority Queue. What is a priority queue? What does it do? Let's go over that.
At a fundamental level, priority queues implement three operations:
You may be thinking: Weird flex, but why does this matter? That's a fair point. The thing that is really interesting with a priority queue is that its optimal implementation has the following runtimes for each operation (and the comparison to a linked list):
I think it's actually pretty important that we go over the implementation details to understand how and why these operations are so efficient.
This is where I usually got lost when someone was explaining this to me. "Binary Heap" sounds terrifying and I certainly think the name makes it sound way worse than it is.
A Binary Heap, at the end of the day, is just an array that we can think about as a certain type of binary tree. Nonono, don't panic, look at the diagram below, it makes sense I promise.
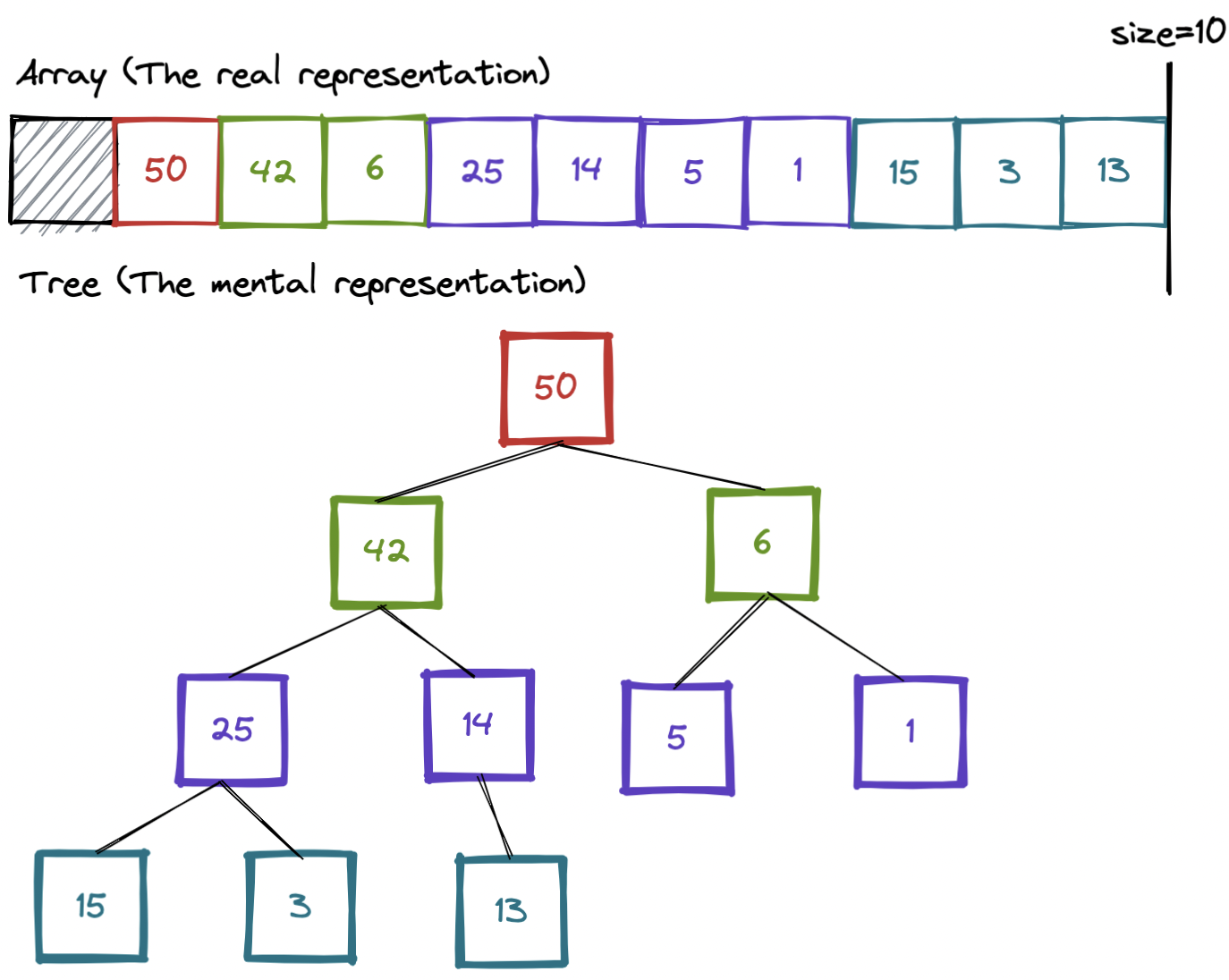I'd like to imagine that this diagram makes the
data structure a lot more clear. We're storing the data as an array (of integers
in this case), no pointers, no other schenanigans. One small note to mention, is
I'm going to make the array based on index 1. To avoid any confusion, I will put
a grayed out block at index 0.
While this diagram is helpful, I should actually cover the real mathematic definition. The "invariable" (the thing that must always be true for this data structure to work) is that any node should be smaller than their parent.
Let's go over some basic operations we can do ("for free") as a result of this structure.
Because this is all bitwise operations, it's super fast for a computer to do!
One small note is that we also store the size of the heap somewhere as well.
This gets important later as it allows us to strategically ignore the last few
elements of the heap.
Let's actually implement the priority queue operations in pseudocode to make
sure that a binary heap fits the bill. We actually only need 2 core procedures
to do everything you could ask for with a binary heap. These two are called
sink and swim, because of how the graph changes at every iteration. Let's go
over each implementation.
Before we start, I should explain two things:
Here's the implementation:
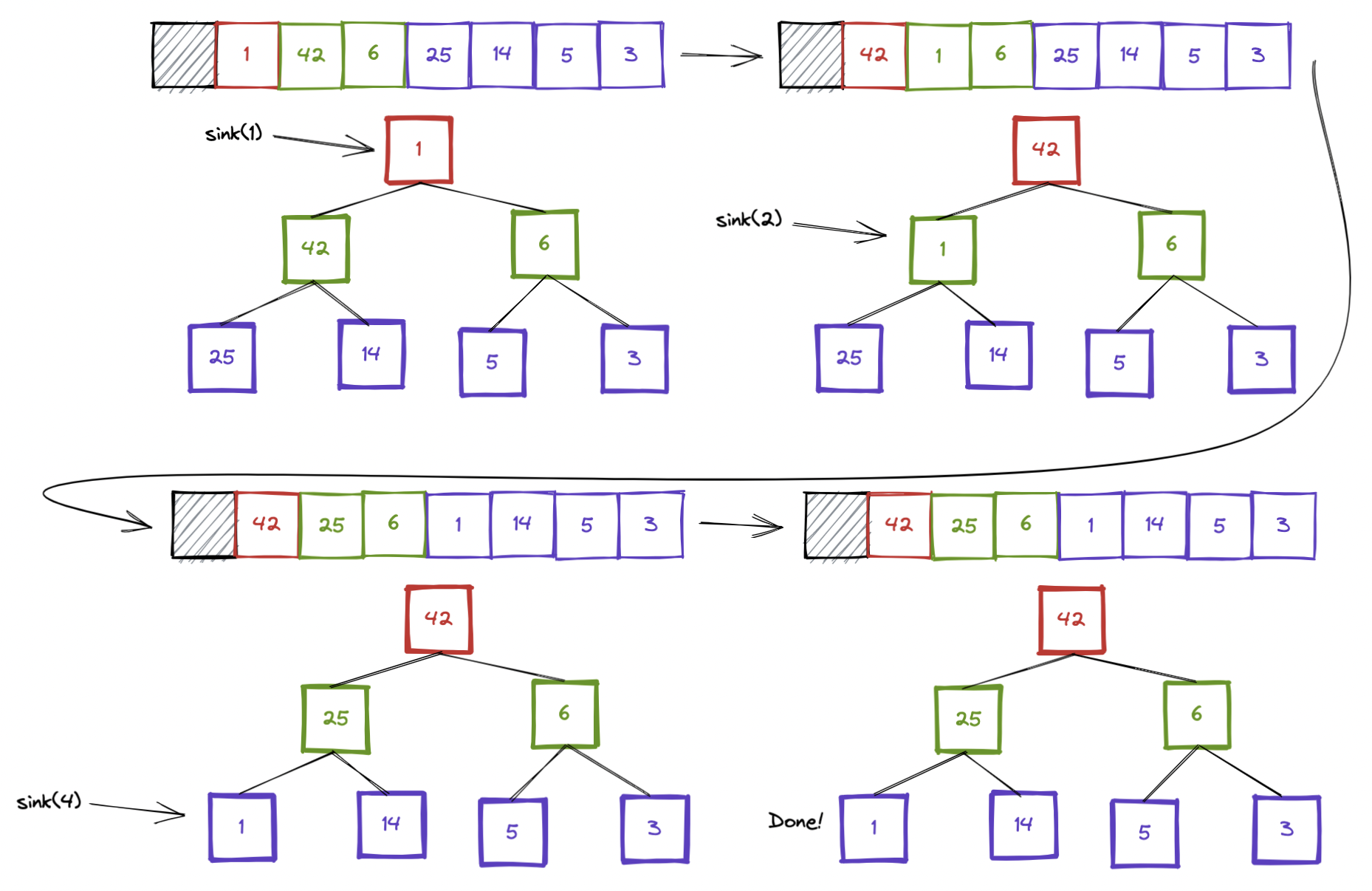
define sink(int index)
1. If a[index] is a leaf (is a node on the last layer of the tree) return
1. This is the base case
2. If a[index] is greater than or equal to the max(a[index*2], a[index*2 + 1]) return
1. There is no problem and this is already a heap
3. let j equal the index of the child with a value larger than my own value
4. swap the elements at index and j
5. Call sink(j)Below is a visualization of this process happening on some arbitrary heap.
Here's the implementation:
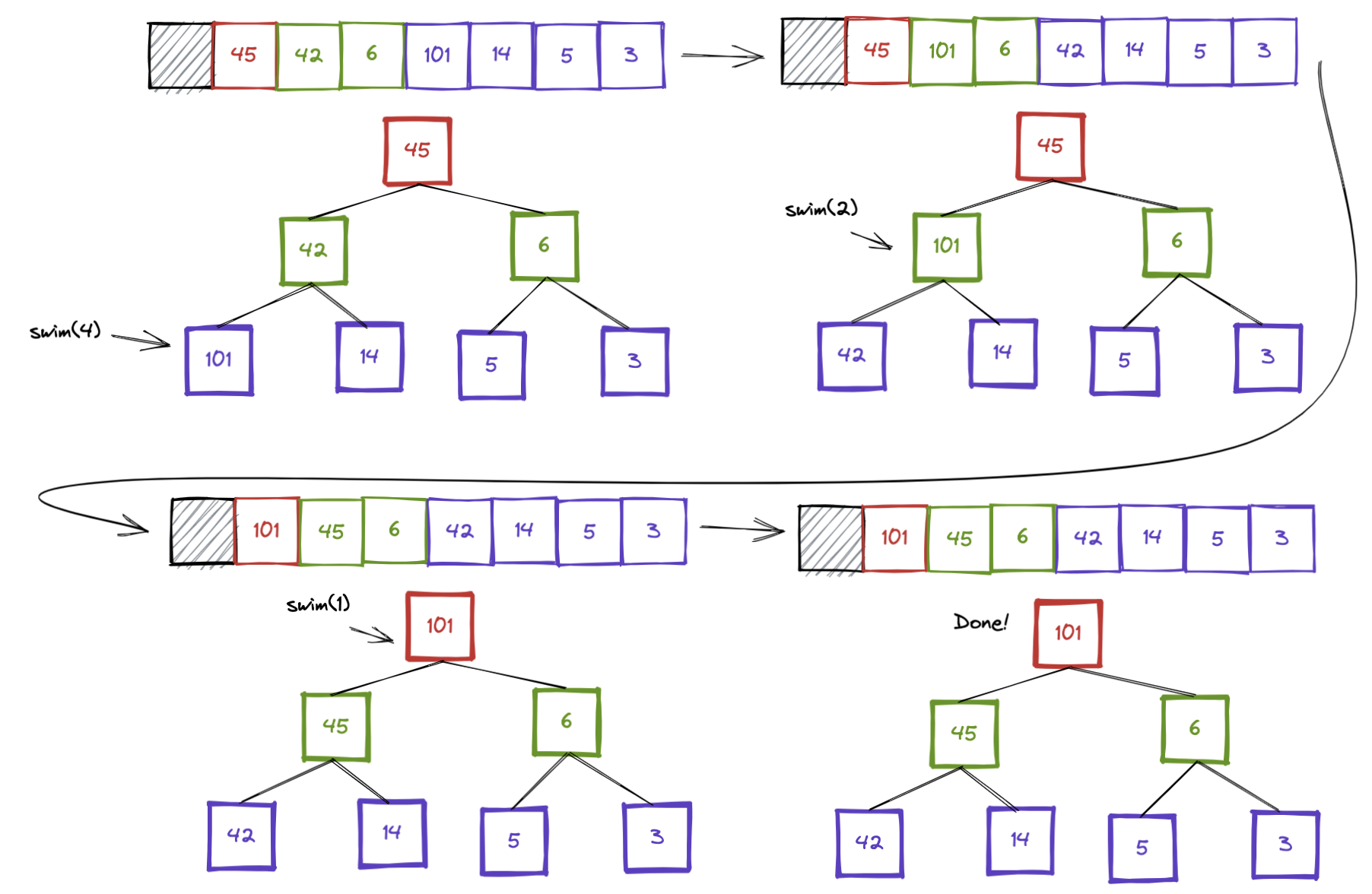
define swim(int index)
1. If index is 1, return
1. This is the base case
2. If a[index] is less than or equal to a[index/2], return
1. There is no problem
3. swap the elements at index and index/2
4. Call swim(index/2)Below is a visualization of this process happening on some arbitrary heap.
Before we move on, I want to mention that both of these procedures run in O(log(n)) time (because they get run once per layer of the tree).
These are actually super simple to implement now that we have the sink and swim procedures. This is also where the size variable that I mentioned earlier comes into play.
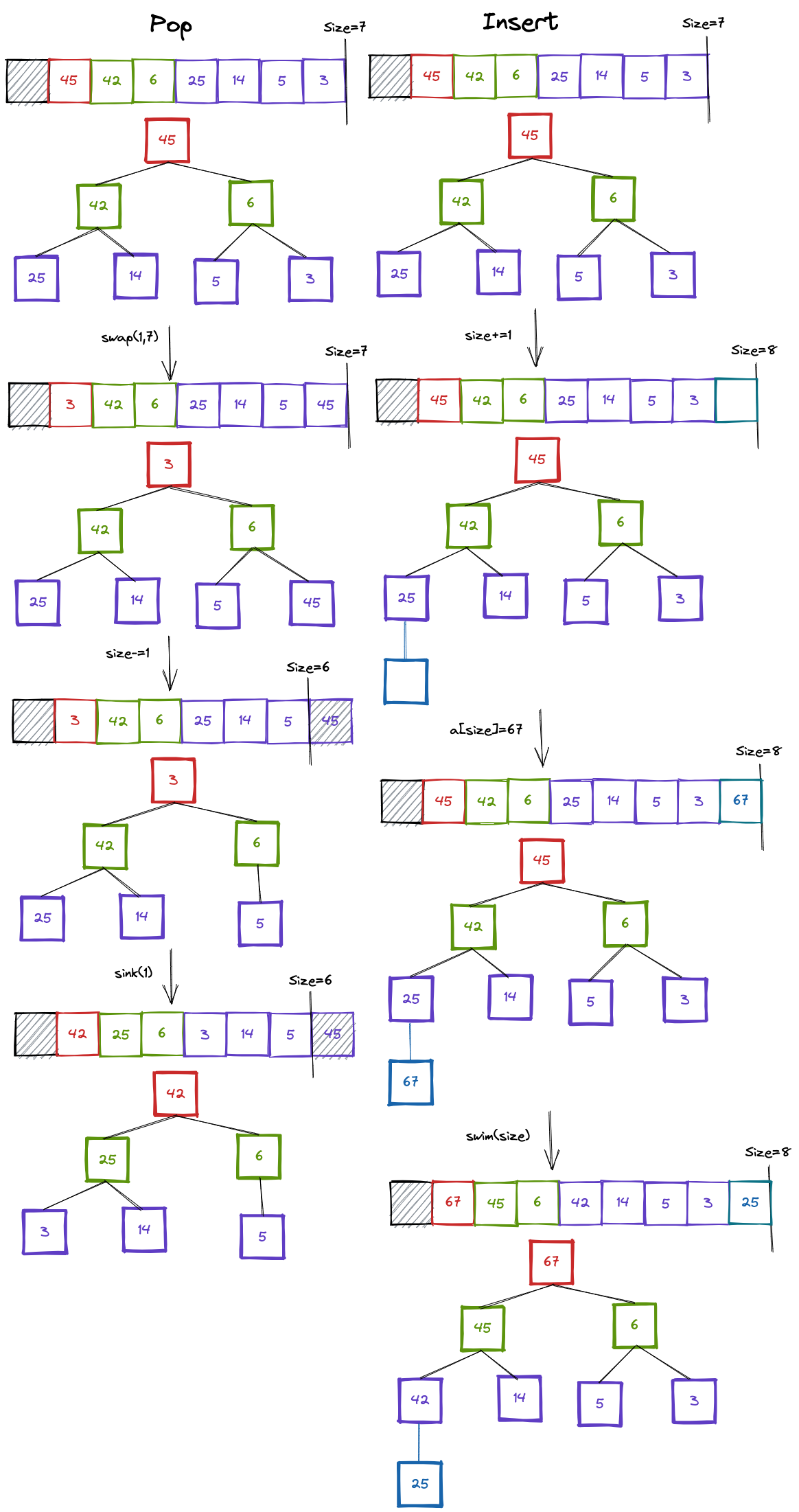
Pop:
1. Swap A[1] with A[size]
2. Decrease size by one
3. sink(1)
4. (optional) return A[size+1] (which is the same thing as the A[1] from the start)Insert:
1. Increase size by one
2. Set A[size] to the number
3. swim(size)If just reading the pseudocode doesn't do it for you, look at this diagram:
We can now see that after all of this
work, we have implemented a binary heap and can move on to the last step before
implementing heapsort. We now have a significantly faster way of accessing and
moving the max number (remember, it runs in log(n) time). If only converting
from an arbitrary array to a binary heap was fast. What if it is?
This is going to be a really short section, but there's one small wrinkle in how this is done that I think is fascinating.
If I asked you right now, off the top of your head, how to turn an arbitrary array with a binary heap, you could probably come up with the following:
1. Create binary heap with enough allocated memory to store the array and set size to 0
2. Run our insert procedure for every element of the input arrayThat not only works, it also runs in O(nlog(n)) time. But we can we do better? Of course we can. With a little bit more thought, you might realize that you don't even need to allocate more memory. You already have an array of the perfect size. You could for instance do:
for index in n
swim(index)That's pretty good! It's still O(nlog(n)), but without any memory allocation it's a pretty smart way of doing it. This is where the average person would stop. How could there be a better way of turning our array into a binary heap? This is where something super non-obvious happens:
for index=n -> 1:
sink(index)Huh. That's interesting (it's weird that we could use sink or swim to do this), but who cares? It turns out that if you do the math for this one, it runs in O(n) time! That's pretty incredible, and is our final step in unlocking the optimal heap sort algorithm.
After coming this far, a lot of people expect that heap sort is going to be some brutal, ungodly algorithm. This is not the case. Heap sort consists of two steps:
1. Convert input array to a binary heap
2. Run our pop method for every n in the binary heapThat's it! Because we know step 1 can be done in O(n) time (or O(n log(n)) if you're feeling lazy), we are only left we dealing with step 2. We already know however that our pop method runs in O(log(n)) time, which means that step 2 runs in O(n log(n)). What this means is that we just implemented a sorting algorithm that runs in O(n log(n)) time, and we didn't even need any weird pivot nonsense.
If you're interested in seeing a visualization of what I talked about here,
I recommend this one . It is
unbelievably ugly, but it does explain the concept quite well. One of these days
I might just make my own visualization software. If you just want to see how the
array itself would change following these steps, here's a visualization:
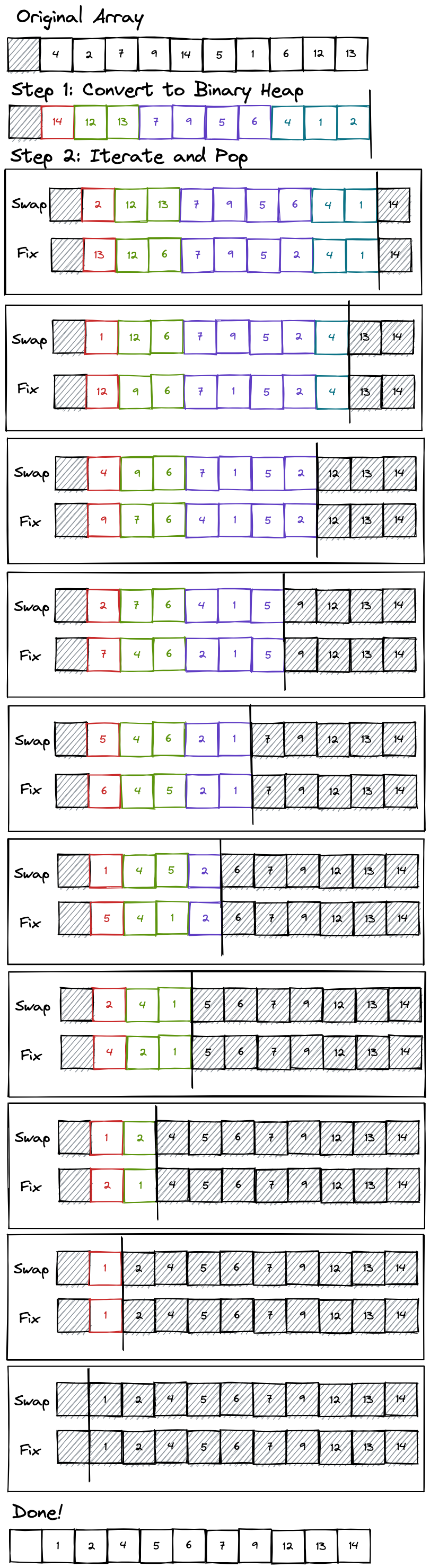
I hope that this has explained or clarified how and why heap sort works, as well as motivated the reasoning on how someone was able to come up with it. If you have any questions or concerns, don't hesitate to reach out to me! I'd love to have a conversation.
Comments